Introduction

In the vast landscape of elementary mathematics education, certain concepts serve as crucial pillars upon which a child's entire mathematical understanding is built. One such fundamental concept is multiplication, which finds its formal introduction in the third-grade Common Core Math Standard 3.OA.A.1. This standard, seemingly simple on the surface, opens up a world of mathematical thinking that will shape students' problem-solving abilities for years to come. Common Core Math Standard 3.OA.A.1 states: "Interpret products of whole numbers, e.g., interpret 5 × 7 as the total number of objects in 5 groups of 7 objects each." At its core, this standard asks students to move beyond mere memorization of multiplication facts and delve into the conceptual understanding of what multiplication truly represents. The importance of this standard cannot be overstated. It marks a pivotal transition in a student's mathematical journey, bridging the gap between the concrete world of counting and addition to the more abstract realm of multiplicative thinking. By mastering this standard, students develop a robust foundation that will support their understanding of more complex mathematical concepts in the future, including:

1. Division (the inverse operation of multiplication)

2. Fractions and decimals

3. Ratios and proportions

4. Algebraic thinking

5. Area and volume calculations

6. Data analysis and statistics

Moreover, this standard encourages students to think flexibly about numbers and their relationships, fostering problem-solving skills that extend far beyond the mathematics classroom. Standard 3.OA.A.1 serves as a crucial building block in students' mathematical development for several reasons:

1. Conceptual Understanding: It moves students from rote memorization to genuine comprehension of multiplication as a mathematical operation.

2. Real-World Connections: By interpreting products, students begin to see how multiplication applies to everyday situations, making mathematics more relevant and engaging.

3. Foundational Thinking: The standard lays the groundwork for understanding more advanced mathematical concepts, including those in algebra and geometry.

4. Problem-Solving Skills: As students explore different ways to represent and solve multiplication problems, they develop critical thinking and problem-solving strategies.

5. Mathematical Communication: The standard encourages students to explain their thinking, fostering important skills in mathematical reasoning and communication.

To help students interpret products of whole numbers, educators typically employ four primary models. Each model offers a unique perspective on multiplication, catering to different learning styles and reinforcing the concept through varied representations:

1. Array Model: This visual model arranges objects in rows and columns, clearly showing the connection between multiplication and repeated addition. For example, 3 × 4 can be represented as three rows of four objects, illustrating both the groups (rows) and the number in each group (columns).

2. Skip Counting: This model leverages students' familiarity with counting to introduce multiplication. For instance, 5 × 3 can be understood by skip counting by 5 three times: 5, 10, 15. This method bridges the gap between addition and multiplication.

3. Repeated Addition: Closely related to skip counting, this model explicitly shows multiplication as a shorthand for adding the same number repeatedly. For example, 4 × 6 can be expressed as 6 + 6 + 6 + 6, reinforcing the concept of "groups of" in multiplication.

4. Equal Groups: This model emphasizes the "groups of" interpretation of multiplication. It can be represented visually or through word problems, helping students understand real-world applications of multiplication. For instance, 3 × 7 might be visualized as three baskets, each containing seven apples.

By exploring multiplication through these diverse models, students develop a comprehensive understanding of the operation, preparing them for the mathematical challenges that lie ahead.

As we delve deeper into the intricacies of Standard 3.OA.A.1, we'll explore how these models are applied in the classroom, common misconceptions students face, and strategies for ensuring mastery of this crucial mathematical concept. Understanding multiplication is not just about learning facts; it's about opening doors to higher mathematical thinking and problem-solving skills that will serve students throughout their academic careers and beyond.

Defining & Interpreting The Standard

3.OA.A.1: Interpret products of whole numbers, e.g., interpret 5 × 7 as the total number of objects in 5 groups of 7 objects each. 

Key Terms

Product-The result of multiplying two or more numbers.

Whole numbers-Natural numbers that include numbers  like 0, 1, 2, 3, 4, and 5 and exclude negative numbers, fractions, and decimals.

Multiplier- The first number in a 2 factor multiplication problem. It indicates the amount or quantity by which the second number in the multiplication problem is to be multiplied.

Multiplicand-The second number in a 2 factor multiplication problem. It indicates the amount or quantity which is to be multiplied.

Array-An arrangement of quantities or objects in rows and columns.

Interpret-(in this context) To explain or make sense of the relationship between the product and the factors (or mutiplier and multiplicand) of a multiplication problem.

Teaching Strategies & Methods

Models for Interpreting Products of Whole Numbers

Using models like arrays, skip counting, repeated addition, and equal groups helps students understand multiplication in various ways. These models offer visual and concrete representations of multiplication, showing the physical grouping of objects and reinforcing the idea of repeated addition of equal groups. They also connect multiplication to skip counting, helping students see the relationship between multiplication and repeated addition. Models like bar models and equal groups aid in understanding multiplication as combining equal parts to form a whole, essential for concepts like area models. By visually representing multiplication facts, models help students derive and internalize facts rather than memorizing them abstractly. Overall, models serve as a bridge from concrete to abstract, allowing students to build a conceptual understanding of multiplication before advancing to larger operations. They make multiplication more accessible and memorable by providing visual representations. In essence, models make multiplication tangible by connecting it to students' prior knowledge and offering visual representations that illuminate the underlying mathematical structure, enhancing comprehension and retention of multiplication concepts.

Array Model

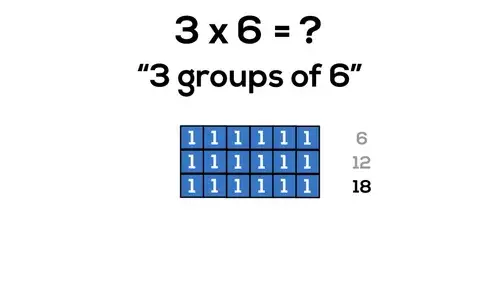
image source: https://makemathmoments.com/progression-of-multiplication/

Description
The array model offers a tangible and visual method for interpreting of products of whole numbers. It provides a concrete way to interpret products of whole numbers and represents multiplication as the arrangement of objects in rows and columns, forming a rectangular array.

How It Works

Draw a grid. The number of columns in your grid should represent first number (the multiplier) and the number of rows should represent to the second number (the multiplicand) in the multiplication problem. Place elements or objects in each cell of the array to represent the individual objects. The total number of elements or objects in the array represents the product of the two whole numbers.

Example

Each factor in a multiplication problem represents rows and columns in the array. Let's multiply 3 x 4. The first factor or multiplier (3) represents the number of rows. The second factor or multiplicand (4) represents the number of columns.

Create the array by drawing the specified number of rows and columns. For 3 x 4, draw 3 rows and 4 columns. The product in this particular multiplication problem is represented by the total number of objects in the array. After counting the total number of objects, you conclude there are 12 total, not only proving 3 x 4 = 12, but visually showing the relationship between the product (12) and the factors (3 and 4).

Imagine your friend gives you 3 bags of apples with 4 apples in each bag. This situation can be represented by an array:

Apples
*           *            *            *
*           *            *            *
*           *            *            *

You have 3 rows.
There are 4 apples in each row.
By counting all the apples in the array, you find a total of 12 apples (3 x 4 = 12).

Benefits

The array model provides numerous advantages for interpreting the products of whole numbers. To begin with, it offers a visual depiction, which aids students in comprehending multiplication as adding repeatedly. Arrays help to better understand the concept of groups of equal size by making it more tangible. They also support the growth of spatial reasoning abilities and can be utilized to present the idea of area, which is intricately connected to multiplication. By using the array model, students gain a more in-depth comprehension of multiplication and the relationship between the product and factors rather than just memorizing facts and establish a strong base for understanding more advanced mathematical ideas.  This model is a powerful tool that helps children visualize and understand multiplication and provides a clear connection between the abstract concept of multiplication and real-world objects, making it more engaging and easier to learn.

Skip Counting Model

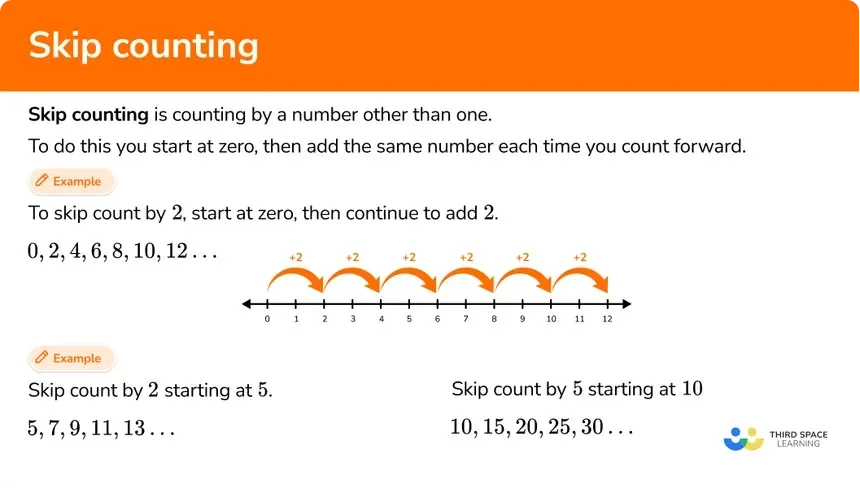
image source: https://thirdspacelearning.com/us/math-resources/topic-guides/number-and-quantity/skip-counting/

The skip counting model is a visual representation of multiplication that involves counting forward by a given number, or 'skip counting.' In this model, the first factor (the multiplier) represents the number of groups, and the second factor (or multiplicand) represents the skip counting increment. The product represents the total number of elements in all the groups combined.This method helps to quickly identify patterns and relationships between numbers. 

How It Works

Start with the first factor, which represents the number of groups. For each group, we skip count by the amount of the second factor. We count the skipped numbers in each group and add them together to arrive at the product.

Example 

Let's find the product of 4 and 5 using the skip counting model. The multiplier or 1st factor (4) represents the number of groups. The multiplicand or 2nd factor (5) represents the skip counting increment. We skip count (starting with the number 5) and count by 5s four times:

5, 10, 15, 20

The last number, 20, in the sequence  represents the product: 4 x 5 = 20.

Benefits

The skip counting model offers a tangible, visual representation of multiplication. This helps students grasp the concept of multiplication and how factors are connected to the final answer. Students develop a more profound grasp of the product by tallying the omitted numbers as it signifies the total elements in the groups, beyond mere rote memorization. The skip counting method is versatile and can be applied to solve multiplication problems with any combination of factors, including those that are challenging to multiply using memorization. When confronted with multiplication issues, students have the option to employ the skip counting method to make an educated guess or approximation of the answer, which can aid in estimating and verifying solutions. The skip counting model connects multiplication to repeated addition and counting patterns. This helps students see the underlying concepts behind multiplication and build a more comprehensive understanding.

Repeated Addition Model

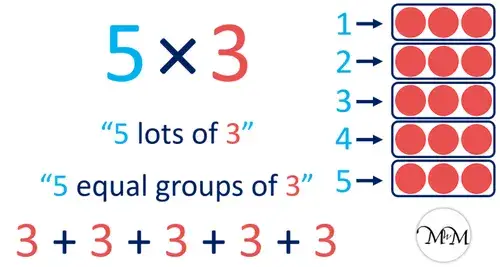
image source: https://www.mathswithmum.com/multiplication-as-repeated-addition/

The repeated addition model of multiplication conceptualizes multiplication as the repeated addition of a specific number. It is a fundamental strategy for students to develop an understanding of multiplication before advancing to more complex models. Begin at the zero point on the number line and advance a certain number of steps equal to the value of the first factor. Next, leap ahead by the amount of times indicated by the second factor. The product is represented by the final point on the number line.

How it Works

In the repeated addition model, the original or first number (multiplicand) is added to itself multiple times, equivalent to the number of times specified by the other or second number (multiplier) in the multiplication problem.

Example
 3 x 5 can be represented as: 5 + 5 + 5 = 15

Benefits

Lays a concrete foundation: Allows students to visualize the concept of multiplication as repeated addition. Builds number sense: Helps students develop an understanding of number relationships and place value. Enhances problem-solving: Provides a tool for solving real-world multiplication problems involving repeated addition.

Equal Groups Model

image source: https://www.splashlearn.com/math-vocabulary/counting-and-comparison/equal-groups

The equal groups model is a visual representation of multiplication that uses the concept of combining equal-sized sets. It interprets the product of two whole numbers as the total number of objects in a defined number of groups, each containing the same number of objects. To understand the product, you would visually count the total number of objects across all groups. This model can be helpful for understanding multiplication as repeated addition, as the product represents the sum of the objects in each group.

How It Works

Draw a set of squares or circles, representing the equal groups based on the first whole number in the multiplication problem. The amount of dots or objects you draw inside each square or circle will be based on the second whole number in the multiplication problem. Calculate product or the total number of items or objects in the entire set by adding all the items in each group. This product represents the answer to the multiplication problem.

Example

Let's consider the multiplication problem 4 x 5. Using the equal groups model, we would represent it as 4 groups with 5 objects each group. Draw 4 circles, draw 5 objects in each circle. Counting the total number of objects in all four circles, we arrive at 20 which demonstrates how multiplying 4 and 5 is the same as adding 5 four times (5 + 5 + 5 + 5 = 20).

Benefits

The equal groups model offers several benefits for interpreting the product of whole numbers. First, it provides an actual visual representation of multiplication, making it easier for learners to grasp the concept. Next, it strengthens the connection between multiplication and repeated addition, reinforcing the fundamental understanding of the operation. Finally, the model promotes reasoning and problem-solving skills, as learners can use it to solve multiplication problems by visualizing and counting the objects in groups. This hands-on approach enhances both conceptual understanding and computational fluency.

Real-World Application

Array Model

Example: Classroom Seating Arrangement Scenario: The teacher wants to rearrange the classroom with 5 rows of desks, each row containing 6 desks.

Application:

• Students can visualize the classroom layout as an array.

• They can calculate the total number of desks: 5 x 6 = 30 desks.

• This example also introduces the concept of area, which they'll study more in later grades.

Activity: Have students draw their ideal classroom layout using an array model, then calculate how many students it can accommodate.

Skip Counting

Example: Counting Money Scenario: Sarah is saving quarters for a new toy that costs $10.

Application:

• Students can skip count by 25 (cents) to determine how many quarters Sarah needs.

• They'll count: 25, 50, 75, 100, 125, 150, 175, 200, 225, 250, 275, 300, 325, 350, 375, 400.

• They'll find that 40 quarters make $10 (40 x 25 cents = 1000 cents = $10).

Activity: Provide students with play money and have them practice skip counting with different coin values to reach various dollar amounts.

Repeated Addition

Example: Grocery Shopping Scenario: Mom needs to buy 6 cartons of eggs, and each carton costs $3.

Application:

• Students can use repeated addition to calculate the total cost: 3 + 3 + 3 + 3 + 3 + 3 = 18

• They can then relate this to multiplication: 6 x $3 = $18

Activity: Create a mock grocery store in the classroom. Give students a shopping list with multiple quantities of items and have them calculate the total cost using repeated addition, then multiplication.

Equal Groups

Example: Planting a Garden Scenario: The class is planting a small vegetable garden. They have 4 types of vegetables, and they want to plant 8 seeds of each type.

Application:

• Students can visualize 4 equal groups of 8 seeds each.

• They can calculate the total number of seeds needed: 4 x 8 = 32 seeds

Activity: Have students design their own garden plots, deciding how many rows of each vegetable they want to plant and calculating the total number of plants.

Combining Models: School Bus Seating

This example combines array, skip counting, and equal groups models.

Scenario: The school has 6 buses for a field trip. Each bus has 5 rows of seats, with 2 students per row.

Application:

• Array: Each bus seating is an array of 5 rows and 2 columns.

• Skip counting: Students can find the number of students per bus by skip counting by 2s: 2, 4, 6, 8, 10.

• Equal groups: The 6 buses represent 6 equal groups.

• Final calculation: 6 x (5 x 2) = 6 x 10 = 60 students total

Activity: Have students create a seating chart for their own imaginary bus fleet, calculating how many students they can transport for a big school event.

Real-world Problem Solving: School Lunch

This example incorporates multiple models and real-world problem-solving.

Scenario: The school cafeteria needs to prepare lunch for 3 third-grade classes. Each class has 24 students. The lunch includes 3 chicken nuggets per student.

Application:

• Equal groups: 3 classes of 24 students each.

• Repeated addition or multiplication to find total students: 24 + 24 + 24 or 3 x 24 = 72 students

• Skip counting by 3s or multiplication to find total nuggets: 3 x 72 = 216 nuggets needed

Activity: Have students plan a class party, determining how many of each item they need based on the number of students and the servings per student.

These real-world examples help students see the practical applications of multiplication in their daily lives. By presenting these scenarios and engaging students in related activities, teachers can make abstract mathematical concepts more concrete and meaningful for 3rd graders.

Common Misconceptions & Challenges

Array Model

Misconceptions:

• Students may think the order of factors doesn't matter in an array.

• They might confuse rows and columns.

Challenges:

• Transitioning from concrete objects to a more abstract array representation.

• Understanding that an array represents multiplication, not addition.

Example: Consider 3 x 4 = 12

[● ● ● ●]

[● ● ● ●]

[● ● ● ●]

Misconception: A student might think this represents 4 x 3 instead of 3 x 4.

Solution: Teach students to consistently read arrays from left to right, emphasizing that the first number represents rows and the second represents columns. Practice creating and describing arrays using both physical objects and drawings.

Skip Counting

Misconceptions:

• Students may not connect skip counting to multiplication.

• They might struggle when starting from a number other than zero.

Challenges:

• Applying skip counting to solve real-world problems.

• Recognizing patterns in skip counting sequences.

Example: 5 x 3 = 15

Misconception: A student might count "5, 10, 15" but not understand how this relates to 5 x 3.

Solution: Use a number line to visually represent skip counting. Show how each jump represents one group of the number being multiplied. Emphasize the connection between the number of jumps and the multiplier.

Repeated Addition

Misconceptions:

• Students might always write the larger number first in repeated addition.

• They may not understand that repeated addition is the same as multiplication.

Challenges:

• Transitioning from repeated addition to more efficient multiplication strategies.

• Applying repeated addition to word problems.

Example: 4 x 6 = 24

Misconception: A student might write 6 + 6 + 6 + 6 instead of 4 + 4 + 4 + 4 + 4 + 4.

Solution: Demonstrate both ways of writing repeated addition for the same problem. Use physical objects or drawings to show that both representations result in the same total. Gradually introduce the multiplication symbol as a shorthand for repeated addition.

Equal Groups

Misconceptions:

• Students might think groups always need to be arranged in a specific way.

• They may struggle to see equal groups in real-world contexts.

Challenges:

• Recognizing equal groups in various arrangements and contexts.

• Understanding that the total is the product of the number of groups and the size of each group.

Example: 3 x 4 = 12

Misconception: A student might only recognize equal groups when objects are neatly arranged in rows or columns.

Solution: Present equal groups in various arrangements (circular, scattered, etc.) to emphasize that the arrangement doesn't change the total. Use real-world examples like egg cartons, muffin tins, or packs of gum to illustrate equal groups in everyday life.

General strategies to address these misconceptions and challenges:

1. Use manipulatives and visual aids consistently across all models.

2. Encourage students to explain their thinking and reasoning.

3. Provide plenty of real-world examples and word problems.

4. Show connections between different models (e.g., how an array relates to equal groups).

5. Practice transitioning between concrete, pictorial, and abstract representations.

6. Use number talks to develop mental math strategies based on these models.

By addressing these misconceptions and challenges, teachers can help students develop a strong foundation in multiplication, setting them up for success in more advanced mathematical concepts.

Assessment of Understanding

Informal Assessments:

Exit Tickets Description: At the end of a lesson, give students a quick problem to solve before leaving class.

Example: Draw an array to represent 4 x 6. Explain how your array shows the product.

Evaluation: Check if students:

• Correctly draw a 4 by 6 array

• Explain that there are 4 rows of 6 dots (or 6 columns of 4 dots)

• Identify the total as 24

This assessment helps gauge students' understanding of the array model and their ability to explain their reasoning.

--

Think-Pair-Share Description: Present a word problem to the class. Have students think individually, then discuss with a partner, and finally share with the class.

Example: Sara is arranging her sticker collection. She has 7 pages in her album, and she wants to put 5 stickers on each page. How many stickers will she use in total?

Evaluation: Observe students as they:

• Identify the problem as a multiplication scenario

• Choose an appropriate strategy (e.g., repeated addition, skip counting, or direct multiplication)

• Explain their reasoning to their partner

• Present their solution method to the class

This assessment allows you to evaluate students' problem-solving skills, their ability to communicate mathematical ideas, and their understanding of real-world applications of multiplication.

--

Whiteboard Quick Checks Description: Ask students to solve problems on individual whiteboards, holding them up for you to see.

Example: Show three different ways to represent 3 x 4.

Evaluation: Look for students to demonstrate:

• An array model

• Repeated addition (4 + 4 + 4 or 3 + 3 + 3 + 3)

• Equal groups (3 groups of 4 or 4 groups of 3)

• Skip counting

• The multiplication sentence

This assessment helps you quickly gauge students' flexibility in representing multiplication and their understanding of different models.

Formal Assessments:

Performance Task: Party Planning Description: Students plan a class party, applying multiplication in a real-world context.

Task: Our class is having a party. We need to buy supplies for 24 students. Each student should get:

• 3 balloons

• 2 party favors

• 5 cookies

a) Calculate how many of each item we need to buy. b) If balloons come in packs of 12, how many packs should we buy? c) Draw an array to show how many cookies we need in total. d) The teacher will bring 4 pizzas. If each pizza has 8 slices, will there be enough for everyone to have 1 slice? Explain your reasoning.

Evaluation: Assess students' ability to:

• Correctly multiply to find totals

• Apply division (for balloon packs)

• Represent multiplication using arrays

• Use multiplication for problem-solving and explanation

This comprehensive task evaluates multiple aspects of multiplication understanding and application.

--

Written Test Description: A traditional paper-and-pencil test covering various aspects of multiplication.

Example Questions:

1. Write a multiplication sentence for this array: [● ● ● ●] [● ● ● ●] [● ● ● ●]

2. Solve: 7 x 6 = ___

3. Draw an equal groups model for 5 x 3.

4. Jenny has 4 boxes of crayons. Each box contains 6 crayons. How many crayons does Jenny have in total?

5. Fill in the blank: 3 + 3 + 3 + 3 = ___ x 3

--

Evaluation: This test assesses students' ability to:

• Interpret arrays

• Perform basic multiplication

• Represent multiplication using models

• Solve word problems

• Connect repeated addition to multiplication

--

Interview Assessment Description: One-on-one interviews with students to deeply assess their understanding and thought processes.

Example Questions:

1. "Can you explain what 4 x 3 means?"

2. "Show me how you would solve 6 x 5 using any method you choose."

3. "Here's a word problem: There are 3 baskets, each containing 7 apples. How many apples are there in total? Can you walk me through how you'd solve this?"

4. "Can you think of a real-life situation where you might use multiplication?"

Evaluation: This assessment allows you to:

• Understand students' conceptual grasp of multiplication

• Observe their problem-solving strategies in real-time

• Assess their ability to apply multiplication to real-world scenarios

• Identify any misconceptions or areas needing additional support

These informal and formal assessments provide a comprehensive view of students' understanding of multiplication. They cover various models (arrays, equal groups, repeated addition) and assess both procedural fluency and conceptual understanding. By using a mix of these assessments, teachers can gain a well-rounded picture of each student's mastery of the 3.OA.A.1 standard and identify areas for further instruction or support.

Conclusion