image source: https://www.math-exercises-for-kids.com/

Introduction 

Developing fluency with multiplication and division within 100 is a crucial skill for 3rd grade students. Being able to apply these basic operations to real-world, contextual word problems helps children build a deeper, more practical understanding of mathematics. When 3rd graders can confidently multiply and divide small numbers, they gain a solid foundation in numerical relationships and can more easily grasp advanced mathematical concepts later on. This fluency also supports their ability to efficiently calculate and reason through multi-step problems, an essential skill for keeping up with the increasing rigor of the curriculum.

Furthermore, solving word problems that involve multiplication and division allows students to see how these basic operations apply to everyday situations. Rather than just practicing the mechanics of the procedures in isolation, 3rd graders can make connections between the math they're learning and the world around them. This makes the content more meaningful and memorable, as students recognize the practical applications of what they're studying. The contextualization also promotes deeper understanding, as children must analyze the details of the problem, determine the appropriate operations to use, and apply them correctly to find the solution.

Additionally, using multiplication and division to solve word problems enhances 3rd graders' overall problem-solving abilities. The process of breaking down a multi-part question, deciding on the necessary steps, and carrying out the calculations develops critical thinking and reasoning skills. Students learn to approach problems methodically, recognize patterns, and apply their knowledge flexibly. These problem-solving strategies are not only crucial for mathematics, but also serve students well as they progress through their education and encounter more sophisticated challenges across all subject areas.

Defining & Interpreting The Standard

3.OA.A.3 states: "Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem."

This standard requires students to:

• Comprehend word problems involving multiplication and division

• Work with numbers up to 100

• Utilize various problem-solving strategies

• Represent problems using mathematical equations

• Apply knowledge to different situational contexts

Key Terms

• Equal Groups

  • Definition: Sets containing the same number of objects

  • Example: 4 bags with 3 apples each represents 4 × 3

• Arrays

  • Definition: Objects arranged in equal rows and columns

  • Example: A 5 × 6 array of chairs in an auditorium

• Measurement Quantities

  • Definition: Numbers representing units of measurement

  • Example: 24 inches divided into 3 equal parts

• Unknown Value

  • Definition: The missing number in an equation

  • Symbol representations: □, ?, or a letter variable

Teaching Strategies & Methods

Visual Modeling: Bar Models

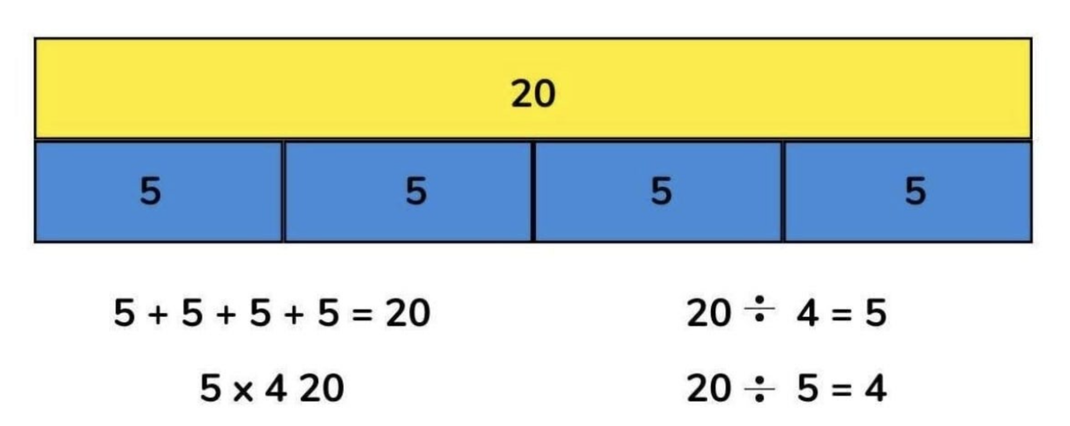
image source: https://thirdspacelearning.com/blog/bar-model-multiplication-division/

Visual Modeling Strategy in real-world contexts means using pictures, diagrams, or drawings to represent mathematical relationships in everyday situations. This strategy helps students translate abstract mathematical concepts into concrete visual representations they can analyze and manipulate. When students encounter word problems, visual modeling allows them to create a picture or diagram that shows the relationships between quantities, making the problem's structure more apparent. In real-world scenarios, this might involve drawing boxes to represent containers, circles to represent groups of objects, or lines to show equal partitioning of items. The strategy is particularly powerful because it helps students bridge the gap between the written word problem and its mathematical solution by providing a visual intermediate step that makes the problem's structure more transparent.

Bar models are powerful tools that help students solve word problems by:

• Visualizing Relationships: Students can see how parts relate to the whole

• Understanding Equal Parts: The bar's divisions clearly show equal portions

• Identifying Operations: The model's structure helps determine whether to multiply or divide

Example Problem: "There are 24 cookies packaged equally in 3 boxes. How many cookies are in each box?"

Process Using Bar Models:

1. Draw one long rectangle representing all 24 cookies

2. Divide the rectangle into 3 equal sections (boxes)

3. Write "24" above the whole bar

4. Label each section with "?" to represent the unknown amount

5. Set up equation: 24 ÷ 3 = 8

This method helps students because:

• They can physically see the division of the whole into equal parts

• The visual representation makes the abstract concept concrete

• Students can check their answer by seeing if the parts equal the whole

Visual Modeling: Array Drawings

https://www.hmhco.com/blog/teaching-relationship-between-multiplication-division-using-arrays

Arrays help students understand multiplication and division by:

• Showing Equal Groups: Each row or column contains the same amount

• Demonstrating Commutative Property: Students can see that 4 × 6 equals 6 × 4

• Supporting Skip Counting: Students can count by rows or columns

Example Problem: "A classroom has 5 rows of desks with 6 desks in each row. How many desks are there total?"

Process Using Arrays:

1. Draw 5 rows of dots/squares

2. Put 6 dots/squares in each row

3. Count total or multiply: 5 × 6 = 30

Benefits include:

• Visual representation of equal groups

• Clear organization of quantities

• Easy verification of answers through counting

Number Line Strategy

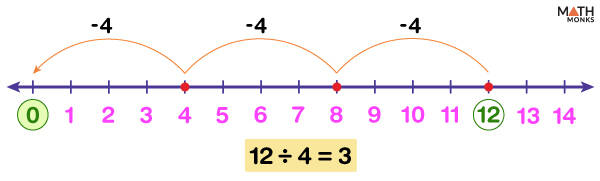
The Number Line Strategy in real-world applications involves using a linear representation to show how quantities increase or decrease in equal amounts, much like measuring distance or tracking progress. This approach is especially useful when dealing with real-world situations involving sequential or cumulative quantities. Using number lines helps students visualize how numbers relate to each other in space and how operations change quantities. In practical applications, number lines can represent everything from timeline progressions to distance measurements to equal grouping situations. This strategy is particularly effective because it shows both the process and the result of mathematical operations, allowing students to see how they get from the starting point to the final answer through equal steps or jumps.

Number lines help solve word problems by:

• Showing Movement: Students can "jump" forward or backward

• Visualizing Skip Counting: Equal jumps represent repeated addition/subtraction

• Demonstrating Division: Equal partitioning of a line segment

Example Problem: "A teacher has 28 pencils to distribute equally among 7 students. How many pencils will each student receive?"

Process Using Number Lines:

1. Start at 0

2. Make jumps of equal size to reach 28

3. Count the number of jumps needed

4. Each jump represents one student's share

This helps students by:

• Making the division process visible

• Showing equal grouping clearly

• Supporting understanding of repeated subtraction

Manipulative Strategy

image sourec: https://www.prodigygame.com/main-en/blog/math-manipulatives/

The Manipulatives Strategy in real-world contexts involves using physical objects or digital representations to model mathematical situations that students might encounter in their daily lives. This hands-on approach allows students to physically create and manipulate groups, arrays, or sets that represent real-world quantities. The strategy transforms abstract numbers into tangible objects that students can move, group, and count. In practical applications, manipulatives might represent anything from coins and dollars to items being shared among people to objects being organized into equal groups. This approach is especially powerful because it allows students to experiment with different arrangements and physically experience the process of solving problems, making abstract mathematical concepts concrete and meaningful.

Physical manipulatives support problem-solving by:

• Creating Concrete Representations: Students can touch and move objects

• Allowing Experimentation: Students can try different groupings

• Supporting Multiple Methods: Objects can be arranged in various ways

Example Problem: "If each craft project needs 4 buttons, how many projects can be made with 20 buttons?"

Process Using Manipulatives:

1. Count out 20 buttons

2. Create groups of 4 buttons

3. Count the number of complete groups

4. Set up division equation: 20 ÷ 4 = 5

Benefits include:

• Hands-on learning experience

• Immediate feedback through physical grouping

• Support for visual and kinesthetic learners

Story Content Creation

Story Context Creation as a strategy involves students generating their own word problems based on real-life situations they understand and can relate to. This approach goes beyond simply solving given problems by requiring students to think about how multiplication and division appear in their daily lives. When students create their own contextual problems, they must think deeply about the relationship between mathematical operations and real-world situations. This strategy helps students understand not just how to solve problems, but why certain operations are appropriate for specific situations. It's particularly effective because it requires students to think about mathematics from multiple perspectives – as both problem solvers and problem creators – which deepens their understanding of how mathematical operations relate to real-world situations.

Teaching students to create their own word problems helps by:

• Deepening Understanding: Students must think about operations in reverse

• Developing Mathematical Language: Students practice using math vocabulary

• Building Real-World Connections: Students draw from their experiences

Process for Story Creation:

1. Give students an equation (e.g., 6 × 4 = 24)

2. Have them identify real-world situations where this equation applies

3. Guide them in writing clear, complete word problems

4. Have peers solve each other's problems

Example Student Process:

1. Start with equation: 6 × 4 = 24

2. Think of real situation: Soccer team uniforms

3. Create problem: "A soccer coach needs to order 6 uniforms for each of the 4 teams. How many uniforms should the coach order in total?"

This method helps students by:

• Reinforcing understanding of operations

• Developing critical thinking skills

• Making math more relatable

Integrated Multiple Representations (IMR) Method

This comprehensive approach combines multiple strategies by:

• Using Multiple Formats: Words, pictures, symbols, and numbers

• Connecting Representations: Showing how different methods relate

• Supporting Different Learning Styles: Providing various entry points

Example Problem: "A baker makes 36 cupcakes and puts them equally into 9 boxes. How many cupcakes are in each box?"

IMR Process:

1. Write equation: 36 ÷ 9 = ?

2. Draw bar model showing 36 divided into 9 parts

3. Use manipulatives to physically divide objects

4. Create number line jumps from 0 to 36 by 4s

Benefits include:

• Deeper conceptual understanding

• Multiple ways to verify answers

• Support for various learning preferences

Real-World Application

Real-world applications are highly beneficial for helping students solve multiplication and division word problems for several important reasons. Let me explain their significance in detail.

Real-world applications make abstract mathematical concepts concrete and relatable by connecting them to students' everyday experiences. When students encounter problems involving familiar situations like sharing snacks, organizing sports equipment, or planning classroom arrangements, they can draw upon their personal experiences to make sense of the mathematical operations. For example, when a student faces a problem about distributing 24 cookies equally among 6 friends, they can visualize this scenario because they've likely experienced similar situations in their own lives. This familiarity helps them understand why division is the appropriate operation and makes the problem-solving process more meaningful.

These applications also help develop critical thinking and reasoning skills by showing students why and how mathematics is useful in their daily lives. When students see that multiplication and division have practical applications - like calculating the total number of seats in a theater by multiplying rows and columns, or determining how many teams can be formed from a group of students - they begin to understand mathematics as a tool for solving real problems rather than just an abstract academic exercise. This understanding increases engagement and motivation while helping students develop stronger problem-solving strategies.

Furthermore, real-world applications provide natural contexts for practicing multiple representation methods. When working with real situations, students can more easily:

• Draw pictures to represent the problem

• Use physical objects to model the situation

• Create number lines to show the process

• Write equations that match the scenario

• Explain their reasoning using everyday language

This multi-modal approach strengthens understanding and helps students build connections between different mathematical representations.

Real-world applications also help students recognize problem structures and patterns that appear in various situations. For instance, students begin to recognize that problems involving equal groups (like organizing items into containers or forming equal teams) often involve division, while problems involving repeated equal quantities (like calculating total items in equal packages or determining total seating in equal rows) typically involve multiplication. This pattern recognition helps students develop stronger problem-solving skills and become more independent in identifying appropriate operations.

Additionally, real-world contexts help reveal and address common misconceptions. When students work with familiar situations, they're better able to judge whether their answers make sense. For example, if a student calculates that each friend should get 50 cookies when sharing 24 cookies, the real-world context makes it obvious that something went wrong in their calculation. This built-in reality check helps students develop better number sense and self-correction skills.

Finally, real-world applications support the development of mathematical communication skills. When students work with concrete, familiar situations, they find it easier to explain their thinking and justify their solutions. They can use everyday language to describe mathematical relationships and processes, which helps build a bridge to more formal mathematical vocabulary and expressions. This improved communication ability is crucial for demonstrating true understanding of mathematical concepts and operations.

Visual Modeling Strategy

Scenario: Planning a School Garden

• Problem: "The school garden has 6 rows with 8 plants in each row. How many plants are there in total?"

• Solution Method: Draw an array showing 6 rows and 8 columns

• Equation: 6 × 8 = 48 plants

Number Line Strategy

Scenario: Planning a Field Trip

• Problem: "48 students need to be divided equally among 6 chaperones. How many students per chaperone?"

• Solution Method: Use number line jumps to divide 48 into 6 equal groups

• Equation: 48 ÷ 6 = 8 students per chaperone

Manipulatives Strategy

Scenario: Organizing Sports Equipment

• Problem: "There are 35 basketballs to be stored equally in 5 bins. How many basketballs go in each bin?"

• Solution Method: Use counters to physically divide into equal groups

• Equation: 35 ÷ 5 = 7 basketballs per bin

Common Misconceptions & Challenges

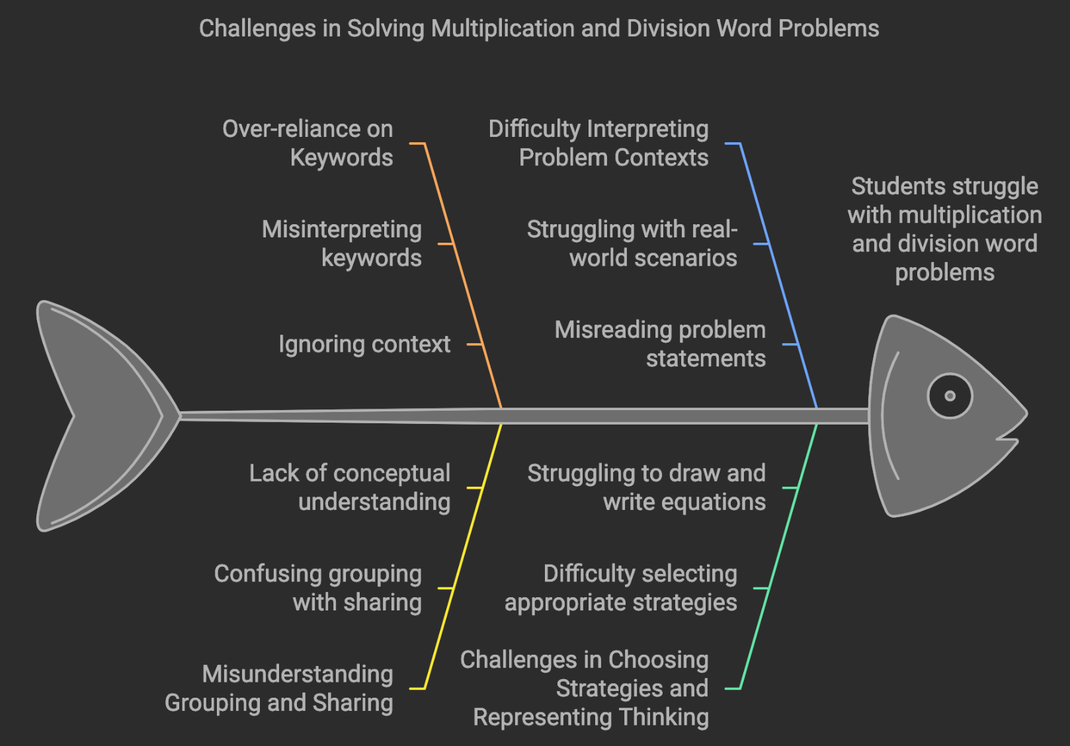
Understanding and solving multiplication and division word problems can present significant challenges for third-grade students as they navigate Standard 3.OA.A.3. As students transition from basic fact fluency to applying these operations in context, they often encounter several common obstacles and misconceptions that can hinder their progress. These challenges range from over-reliance on keywords to misunderstanding the fundamental concepts of grouping and sharing in division problems. Additionally, students may struggle with properly interpreting problem contexts, choosing appropriate solution strategies, and representing their thinking through drawings and equations. Recognizing and addressing these challenges early is crucial for teachers, as these misconceptions can persist and impact students' mathematical development in later grades if left unaddressed. In this section, we'll explore the most common challenges students face when working with multiplication and division word problems, examine why these misconceptions occur, and provide specific strategies and solutions to help teachers guide students toward deeper understanding.

1. Keyword Fixation

Challenge: Students rely too heavily on keywords rather than understanding the problem context.

• Example: Seeing "in all" and automatically multiplying instead of considering if division is needed

• Solution: Teach students to draw pictures or models before choosing an operation

2. Division Interpretation

Challenge: Confusion between partitive (sharing) and quotitive (measurement) division

• Example: Not understanding the difference between "sharing 12 cookies among 3 people" versus "making groups of 3 cookies from 12 cookies"

• Solution: Use different visual models to represent both types of division

3. Array Confusion

Challenge: Misinterpreting rows and columns in arrays

• Example: Confusing 3 × 4 with 4 × 3 arrays

• Solution: Consistently emphasize that the first number represents rows and the second represents columns

Assessment Of Understanding

Effectively evaluating students' mastery of Standard 3.OA.A.3 requires a comprehensive approach that combines both formal and informal assessment methods. Formal assessments play a crucial role in measuring students' understanding of multiplication and division word problems and typically include written tests that require students to solve contextual problems while showing their work through drawings, equations, and written explanations. These assessments often present students with scenarios like sharing stickers among friends or organizing items into equal groups, asking them to demonstrate their problem-solving process and explain their reasoning. Performance tasks serve as another valuable formal assessment tool, challenging students to create their own word problems, represent them visually, and solve them systematically. These tasks not only evaluate students' computational skills but also their ability to understand and apply mathematical concepts in context.

Informal assessments, which are equally important, provide ongoing insights into students' developing understanding and help teachers adjust instruction as needed. Exit tickets serve as quick, end-of-lesson checks that gauge immediate comprehension and identify areas needing clarification. These might involve asking students to draw multiple representations of a multiplication expression or explain their problem-solving strategy. Observation checklists allow teachers to systematically monitor students during group work and independent practice, noting their strategy choices, understanding of concepts, and areas of difficulty. Math journals provide another informal assessment avenue, where students can reflect on their learning, explain their thinking processes, and demonstrate their understanding through writing. These journal entries might include prompts asking students to explain how they determine whether to multiply or divide in word problems, or to describe different ways to represent equal groups.

Formal Assessments

-Written Tests

-Performance Task

  Create a word problem that can be solved using multiplication.  

   Draw a model to represent it.

   Write an equation.

   Solve and explain your solution.

Informal Assessments

-Exit Tickets

  Quick problem-solving checks at lesson end

  Example: "Draw two different ways to show 6 × 4

-Observation Checklists

  Monitor students during group work

  Note strategy choices and problem-solving approaches

-Math Journals

  Students explain their thinking

  Example prompt: "Explain how you know whether to multiply or divide in a word problem"

Conclusion